| information torsion spring
calculation |
|
This spring design program was
created on the basis of the German standard for springs as well as our
experience in production engineering. The computation can be carried out for
compression, extension and torsion springs. The procedures use the same input
logic typical for Windows, i.e. via keyboard and mouse.
No warranty is accepted for calculation results
outside the production at "Gutekunst Federn". |
| pre-setting torsion
spring calculation |
Material, quality category as
per DIN 2194, the properties of the legs and a valid combination of diameter,
spring forces, spring torques and rotating angle must be entered in the
parameter pre-settings.
|
Standard combinations include i.e.:
|
 Material, RH, Di or De, M2, alpha2 Material, RH, Di or De, M2, alpha2 |
 Material, RH, Di oder De, F2,
alpha2 Material, RH, Di oder De, F2,
alpha2 |
 Material, RH, Di oder De, M2, M1,
alpha2 Material, RH, Di oder De, M2, M1,
alpha2 |
 Material, RH, Di oder De, M2, alpha1,
alpha2 Material, RH, Di oder De, M2, alpha1,
alpha2 |
 Material, RH, Di oder De, alpha2, n Material, RH, Di oder De, alpha2, n |
|
 material properties material properties |
Designation,
Material-description
|
Max. operating
temp. |
EN |
F
(AFNOR) |
GB
(BS) |
S
(SIS) |
USA
(AISI) |
| G-module |
EN 10270-1 type SM
Spring steel wire
For all common springs |
80°C |
10270-1 |
NFA
47-301-76 |
BS 5216-75 |
* |
AMS
5112 |
| 81500 |
EN 10270-1 type SH
Spring steel wire
For all common springs |
80°C |
10270-1 |
NFA
47-301-76 |
BS 5216-75 |
* |
AMS
5112 |
| 81500 |
EN 10270-1 type SH and DH
Spring steel wire
For all common springs |
80°C |
10270-1 |
NFA
47-301-76 |
BS 5216-75 |
* |
AMS
5112 |
| 81500 |
EN 10270-2 / VDC
(unalloyed)
Valve spring wire
In high dynamical stress |
80°C |
10270-2 |
* |
* |
* |
* |
| 79500 |
EN 10270-2 / VDSiCr
(alloyed)
Valve spring wire
In high dynamical stress between 80 and 120° C |
120°C |
10270-2 |
* |
2803 685A55HD |
* |
6150 |
| 81500 |
1.4310 /
X10CrNi188
Stainless steel V2A
High corrosion resistance |
270°C |
10270-3 |
Z12CN17.07 |
301S21 |
2330 |
302 |
| 73000 |
1.4568 /
X7CrNiAI17-7
Spring steel V4A
Minimal relaxation, high dynamical stress |
350°C |
10270-3 |
Z8CNA17.07.01 |
301S81 |
2388 |
631 |
| 78000 |
CW507L / CuZn36
Copper wire
Non-magnetic, salt-water proof |
60°C |
12166 |
* |
* |
* |
* |
| 35000 |
CW452K / CuSn6
Bronze alloy
Non-magnetic, solderable, weldable, corrosion
resistant |
60°C |
12166 |
* |
* |
* |
* |
| 39000 |
|
| You have 4 possibilities
for entry: |
 all calculation pre-settings all calculation pre-settings |
Here, all entry windows
for the calculation are available.
|
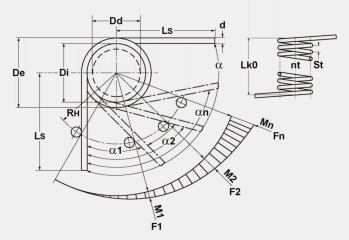
|
RH = distance
between centre of spring body and power flow point on
lever leg (mm) |
| LsH = leg length
of the lever leg (mm) |
| LsR = leg length
of the recumbent leg (mm) |
| Di = inner coil
diameter (mm) |
| De = outer coil
diameter (mm) |
| F1 = prestressed
spring force (N) |
| F2 = loaded
spring force (N) |
| M1 = torque by
angle alpha1 (Nmm) |
| M2 = torque by
angle alpha2 (Nmm) |
| alpha1 =
prestressed rotational angle (degrees) |
| alpha2 = loaded
rotational angle (degrees) |
|
 calculation according to rotational angle and
torque calculation according to rotational angle and
torque |
In this case for a better overview, only the windows
for the calculation according to rotational angle and torque are available.
|
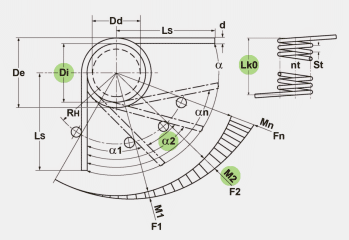 |
RH = distance
between centre of spring body and power flow point on
lever leg (mm) |
| LsH = leg length
of the lever leg (mm) |
| LsR = leg length
of the recumbent leg (mm) |
| Di = inner coil
diameter (mm) |
| De = outer coil
diameter (mm) |
| M1 = torque by
angle alpha1 (Nmm) |
| M2 = torque by
angle alpha2 (Nmm) |
| alpha1 =
prestressed rotational angle (degrees) |
| alpha2 = loaded
rotational angle (degrees) |
|
 calculation according to rotational angle and
spring force calculation according to rotational angle and
spring force |
In this case for a better overview, only the windows
for the calculation according to rotational angle and force are available.
|
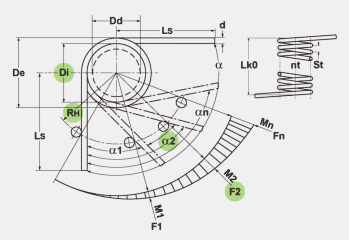 |
RH = distance
between centre of spring body and power flow point on
lever leg (mm) |
| LsH = leg length
of the lever leg (mm) |
| LsR = leg length
of the recumbent leg (mm) |
| Di = inner coil
diameter (mm) |
| De = outer coil
diameter (mm) |
| F1 = prestressed
spring force (N) |
| F2 = loaded
spring force (N) |
| alpha1 =
prestressed rotational angle (degrees) |
| alpha2 = loaded
rotational angle (degrees) |
|
 calculation according to dimension calculation according to dimension |
In this case for a
better overview, only the windows for the calculation according to dimensions
are available.
|

|
RH = distance
between centre of spring body and power flow point on
lever leg (mm) |
| LsH = leg length
of the lever leg (mm) |
| LsR = leg length
of the recumbent leg (mm) |
| Di = inner coil
diameter (mm) |
| De = outer coil
diameter (mm) |
| alpha1 =
prestressed rotational angle (degrees) |
| alpha2 = loaded
rotational angle (degrees) |
| n = number of
active coils (pc.) |
|
|
| result page
compression spring calculation |
Once the computation has been
started from the "Pre-settings", switch automatically to the "results"
computing page which displays all the computed spring sizes.
To
complete the calculation you are requested here to select the wire diameter
< d > according to DIN EN 10218-2 and adapt the number of spring coils < n
> accordingly if required. The nearest five values are available for
selection in the drop-down lists. In the case of torsion springs, adaptation of
the number of coils < n > changes the position of the leg.
The values entered from the "pre-setting" and the wire diameter <
d > can be altered; they are displayed in white highlighted input fields.
All other values are purely output values. The spring is recalculated on the
basis of the modified values using the calculate button.
Invalid or
faulty calculation results are displayed for you in the text box. Solution
possibilities will be presented to you if you click on the individual fault
messages.
Important
The
tension coefficient "k" is incorporated as standard for the torsion spring
computation. The tension coefficient "k" takes approximate account of the
maximum computed tension of the spring body. Furthermore, due to the deflection
of the non-fixed leg (lever leg), the "leg swivel" is included in the
calculation. Bend stresses occurring are ignored !
 |
| leg swivel |
|
Further functions of
torsion spring calculation
Diagrams
The diagrams
function provides you with the path-force diagram and the Goodmann diagram in
the case of dynamic calculation. |
You can print the calculation
or send it as an inquiry direct to Gutekunst Federn. When you have sent your
inquiry you will receive a copy of your inquiry back directly by
e-mail.
You can search our catalogue range directly for a
suitable spring using the < Search catalogue > function. As a standard,
the search program works with a tolerance value of 10%. Please note that our
torsion catalogue springs are only supplied in the material EN
10270-3-1.4310. |
|